Attention is All You Need
Transformer 모델을 만들 때 attention은 매우 중요한 요소 중 하나이다. 사실상 트렌스포머 모델은 attention으로 구성된 encoder-decoder 구조의 아키텍쳐를 의미하는 모델이다. 따라서 트렌스포머를 이해하기 위해서는 attention을 이해하는 것이 필수적이다. 그럼 먼저 attention의 구조에 대해서 살펴보자.

위의 그림만 보아서는 잘 이해가 가지 않으므로, attention의 계산 공식을 먼저 뜯어보도록 하자. Attention은 다음과 같은 계산 공식을 따른다. Attention을 구하기 위해서는 Q, K, V 값이 필요한데, 이는 각각 Query, Key, Value를 의미한다.

이 Q, K, V 값들은 각각 다음과 같다.
Q(Query): 입력 문장의 모든 단어에 대한 벡터K(Key): 입력 문장의 모든 단어에 대한 벡터V(Value): 입력 문장의 모든 단어에 대한 벡터
즉, 정리하자면 Q, K, V 값들은 모두 입력 문장의 모든 단어에 대한 벡터로, 모델이 학습되면서 업데이트된다. Q, K, V 값에 대한 좀 더 자세한 정의를 알아보고 값들이 업데이트되는 과정을 알아보자.
모든 단어는 질문(Query)이자 답변(Key)이다
유명한 예시 중 하나로, "The animal didn't cross the street because it was too tired."라는 문장이 있다. 여기서 it이 가리키는 단어는 무엇일까? 사람들이 문맥상 파악하는 "it"은 "animal"이겠지만, 컴퓨터는 이를 어떻게 알 수 있을까?
이를 알기 위해서 Q, K, V 값들을 사용해야 한다. Q, K, V 값들은 다음과 같이 만들어진다.
step1: 문장의 토큰화
어떤 문장이 주어지면, 토크나이저는 이를 각각의 토큰으로 나눈다. 토큰은 문장을 구성하는 기본 단위로, LLM(Large Language Model)이 인식할 수 있는 문자의 단위를 뜻한다. 어떤 기준으로 토큰을 나누는지는 LLM에 따라서 다르다. 예를 들어, ChatGPT는 영어의 경우에는 단어 단위를 토큰으로 사용한다. 즉 "I am happy"라는 문장이 있다면 토큰은 각각 "I", "am", "happy"가 된다. 그러나 한국어의 경우에는 한 음절당 하나의 토큰으로 처리한다. 즉, "나는 행복하다"에서 토큰은 각각 "나", "는", "행", "복", "하", "다"가 된다.
그러나 네이버에서 만든 HyperCLOVA X의 경우에는 한국어 문장의 최소 단위인 형태소 개념을 사용해 토큰을 구분한다. 즉, "나는 행복하다"에서 토큰은 각각 "나", "는", "행복", "하다"가 된다.
step2: 토큰의 백터화
이렇게 만들어진 토큰은 벡터화된다. 벡터화란 문자열 데이터인 토큰을 숫자로 수치화하는 것인데, 단순히 인덱싱이 아니라 각 토큰의 의미와 연관성을 고려하여 수치화된다. 그 결과로 서로 비슷한 의미를 가지고 있는 토큰끼리는 서로 비슷한 임베딩을 가지게 되며, 서로 연관성이 없는 단어는 유사하지 않은 임베딩을 가지게 된다. 예를 들어 "applicant"와 "application"이라는 단어는 서로 임베딩이 비슷하고, "applicant"와 "zyzzyv"는 서로 임베딩이 많이 달라진다.
이러한 백터화는 대규모 데이터셋에 의해서 사전 훈련된 임베딩 모델에 의해 이루어지기 때문에 이 임베딩 모델이 성능이 뛰어나야 Attention의 성능도 높아진다. ChatGPT는 높은 성능의 임베딩 모델을 가지고 있기 때문에 문장의 맥락을 알아내는 기능도 뛰어난 것이다.

step3: 질문(query)에 대한 답변(key) 알아내기
사전 훈련된 임베딩 모델이 이미 토큰들 간의 연관관계를 잘 알고 있다면, Attention은 왜 필요한 것일까?
다시 처음 예시로 돌아가서 "The animal didn't cross the street because it was too tired."라는 문장을 생각해보자. 여기서 단어 "it"은 대명사이며 이전에 언급되어 있는 명사를 대신해서 지칭하는 단어이다. 임베딩 모델을 사용하면 "it"과 "animal", "street"의 연관성은 높으며, 반대로 "it"과 "because" 등의 단어는 연관성이 낮다는 것은 알 수 있다. 그러나 "it"이 가리키는 단어가 "animal"인지, "street" 인지는 알 수 없다. 이건 문장 내에서의 맥락을 통해서 알아내야 하는 것이기 때문이다.
이러한 맥락을 알아내기 위해서 바로 Q, K, V 값들을 사용한다. 다시 새롭게 Q, K, V에 대한 정의를 공부해보자.
Q(Query): 쿼리 벡터는 다른 모든 단어에 대한 사용되는 현재 단어로, 현재 처리 중인 토큰을 의미한다.K(Key): 키 벡터는 문장의 모든 단어에 대한 레이블로, 임베딩 모델에 의해서 단어를 벡터화시킨 것을 의미한다.V(Value): 값 벡터는 실제 단어 표현으로, 각 단어의 관련성을 평가한 후 현재 단어를 나타내기 위해 업데이트되는 값이다.
즉, 쿼리는 지금 당장 처리하고 있는 토큰의 벡터를 의미한다. Attention은 문장이 주어지면 첫 토큰부터 마지막 토큰까지 순서대로 처리하는데, 이 과정에서 현재 처리하고 있는 토큰이 쿼리가 된다. 예를 들어서 "The animal didn't cross the street because it was too tired." 문장에서 현재 "it"을 검사중이라면, 이 "it"의 벡터값이 바로 쿼리가 된다.
키 벡터는 다른 모든 토큰의 벡터를 의미한다. 위의 문장에 있는 모든 토큰인 "The", "animal", ..., "tired"에 대한 벡터값이 바로 키 벡터가 된다. Attention 모델은 이렇게 현재 처리 중인 토큰의 벡터를 쿼리로, 다른 토큰들의 벡터를 키로 둔 다음, 둘 사이의 유사도(Weight, 가중치)를 계산한다. 예를 들어서 "animal"과 "it"은 임베딩 모델에 의해서 임베딩된 벡터값이 비슷했을 것이므로 유사도도 높게 계산되고, "animal"과 "because"은 반대로 유사도가 낮게 계산된다.
이렇게 계산된 유사도는 단어의 실제 표현값인 Value 백터에 곱해진다. 따라서 결과값인 Value 백터는 문장 내의 단어들 간의 관련성이 모두 표현된 값으로 업데이트되게 된다.
이러한 쿼리 과정을 단순히 "it" 토큰 뿐만 아니라, 문장 내의 모든 토큰에 대해서 거치므로, 최종적으로 Value 백터는 "모든 토큰이 다른 모든 토큰들에 대해서 얼마나 유사한지"를 나타내는 값이 된다. 바로 이러한 과정을 통해서 "it"이 가리키는 단어가 "animal"인지, "street"인지를 구분할 수 있게 된다. "it"과 "animal"의 유사성만 일대일 비교하는 게 아니라, "cross", "tired"와 같은 단어들도 "it"과 "animal"이 얼마나 유사한지를 평가할 수 있게 도와주기 때문이다. 이런 과정을 통해서 "it"의 Attention은 "animal"에 집중된다.
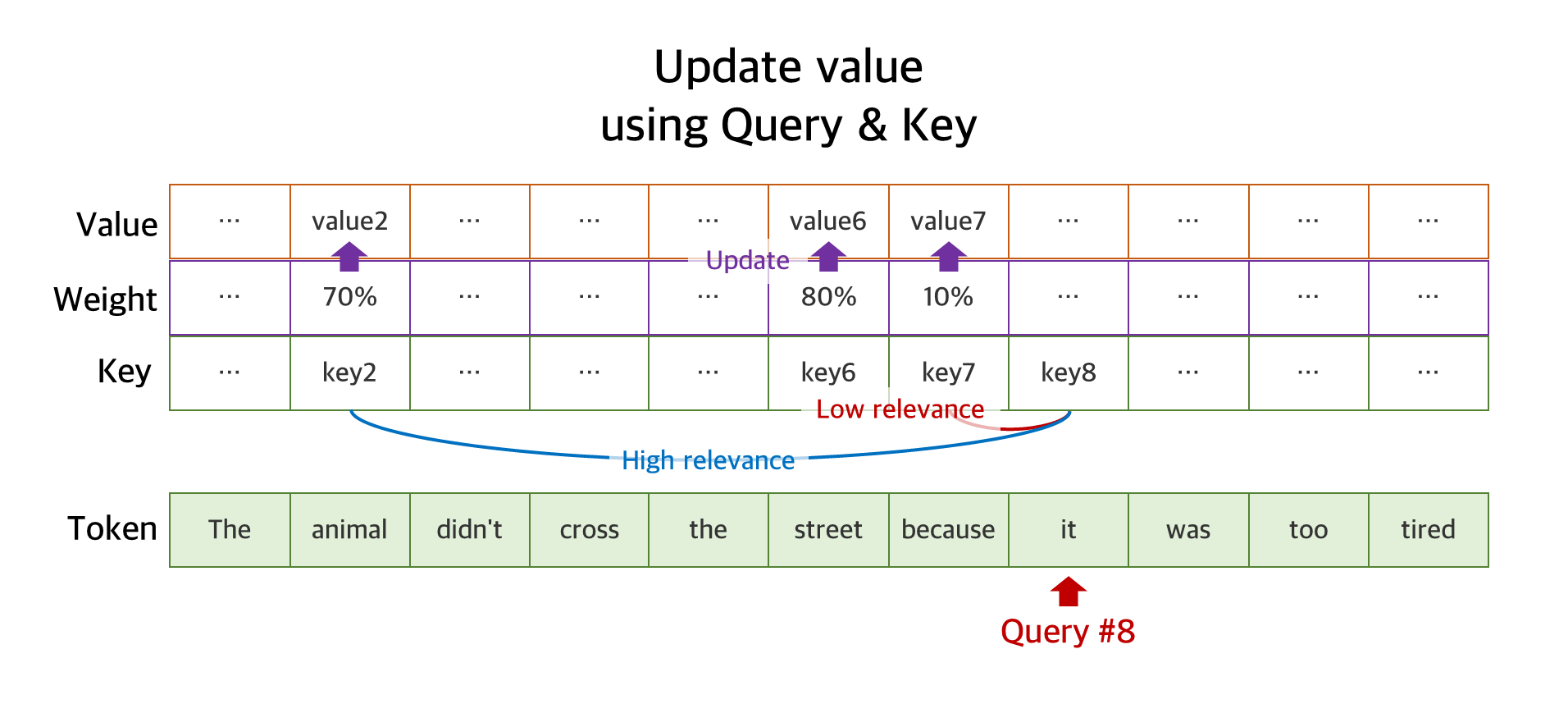
즉, Attention을 정리하자면 다음과 같다.
- 토큰을 앞에서부터 검사하며, 이 토큰의 질문(query)에 대한 다른 토큰의 답변(key)이 얼마나 유사한지 검사한다.
- 이 유사도는 가중치(Weight)로 변환되어 토큰의 현재 값(Value)에 곱해진다.
- 모든 토큰에 대한 검사가 이루어지면, 토큰의 현재 값(Value)은 결과적으로 "모든 토큰이 다른 모든 토큰들에 대해서 얼마나 연관성이 있는지" 알 수 있는 값으로 업데이트 된다.
Attention 계산 공식 수학적으로 살펴보기
이제 Attention과 Q, K, V이 각각 무엇이고 어떻게 업데이트되는지 알아보았으므로, 맨 처음에 나왔던 Attention 계산 공식을 수학적으로 살펴보자.

계산 공식이 의미하는 바는 다음과 같다. 먼저, K 위에 붙어 있는 T는 전치 행렬(Transpose)를 의미한다. 즉, K가 2X3 행렬이었다면 이를 3X2로 바꾸어준다는 의미이다. 이렇게 전치된 K는 Q와 곱해지는데, 이렇게 본래의 Q와 전치된 K가 곱해지는 것을 백터의 내적이라고 한다. 즉, Q⋅TK는 Q와 K의 내적을 나타내는 표기법이다.

여기서 잠깐, 두 벡터를 내적(Dot Product)하는 것의 수학적인 의미를 알아보자. 기하와 벡터에서 공부했듯이, 어떤 두 벡터 a와 b를 내적하면, 그 결과는 ∣a∣⋅∣b∣⋅cos(θ)가 된다. 위의 그림에서 볼 수 있듯이, 이는 두 개의 벡터가 있을때 한 벡터의 방향으로 나머지 하나를 projection(투영)시킨 것(그림자와 비슷하다고 생각하면 된다)과 다른 한 벡터의 크기의 곱이 된다.
결과적으로 이는 두 벡터가 얼마나 비슷한 방향을 취하고 있는지를 나타내게 된다. 벡터의 내적은 그래서 서로 수직하는 경우에는(즉, 방향이 전혀 비슷하지 않을 때는) 0이 되고, 서로 반대방향인 경우에는(즉, 방향이 아예 연관성이 없을 경우) 음수 값이 된다. 즉, 머신러닝과 데이터 분석에서 두 백터를 내적해주는 경우는 주로 유사성이나 관련성을 알기 위해서이다. 지금 우리의 상황에서는 Query와 Key의 유사도를 구하기 위해서 두 벡터를 내적하는 것이다.
이렇게 구한 유사도를 다시 루트 dk로 나누어주는 이유는 그라디언트(gradient)의 크기를 보정하여 학습의 안정성을 높이기 위해서이다. Q⋅TK의 값이 크면 클 수록 출력값이 작아지는 효과를 줄 수 있다. 예를 들어서 가중치 100은 2로 나누면 50이 되고, 가중치 50은 2로 나누면 25가 된다. 나누기 전에는 100-50=50 만큼의 차이가 있었다면, 나눈 후에는 50-25=25 만큼의 차이만 있다. 이처럼 값들이 넓게 분포되어 있던 정도를 스케일링하여 분포를 좁히는 역할을 할 수 있다.
이렇게 쿼리(Q)와 키(K)를 내적(Dot product)하여 유사도를 구하고, d로 나누어 스케일링(Scale)된 최종 가중치를 구한 다음, 이를 값(V)에 곱해주어 값을 업데이트하는 방식을 Attention 메커니즘이라고 한다. 좀 더 정확하게 말하자면 여기까지의 과정은 스케일드 닷 프로덕트 어텐션(Scaled dot-product Attention)이라고 한다. 이름 자체에 메커니즘에 필요한 연산들을 전부 설명한 셈이다.
Self-Attention
그렇다면 Self-Attention은 무엇일까? Self-attention은 같은 문장 내에서 단어들 간의 의미 관계를 고려하는 것을 말한다. 위에서 설명한 "The animal didn't cross the street because it was too tired." 예시가 바로 Self-Attention이다. 즉, 스케일드 닷 프로덕트 어텐션(Scaled dot-product Attention)을 같은 문장 내에서 진행하면 Self-Attention이 된다. 이러한 Self-Attention을 여러 개 만들어 다양한 feature에 대해 검사할 수 있게 만든 것을 Multi-Head Attention이라고 하는데, 이는 다음 기회에 알아보도록 하자.
참고 글
The Illustrated GPT-2 (Visualizing Transformer Language Models)
Discussions: Hacker News (64 points, 3 comments), Reddit r/MachineLearning (219 points, 18 comments) Translations: Simplified Chinese, French, Korean, Russian, Turkish This year, we saw a dazzling application of machine learning. The OpenAI GPT-2 exhibited
jalammar.github.io
'🤖AIML' 카테고리의 다른 글
| [Keras] keras.layers.Dropout 레이어 이해하기 (0) | 2024.02.21 |
|---|---|
| [Keras] keras.layers.Flatten 레이어 이해하기 (0) | 2024.02.19 |
| [Keras] keras.layers.Dense 레이어 이해하기 (0) | 2024.02.19 |
| 이진 분류 및 멀티 클래스 분류에서 TP, TN, FP, FN, Recall, Precision, Accuracy 계산하기(Binary Classification & Muti-class Classification) (0) | 2024.01.19 |
| 리눅스에서 Anaconda 설치 및 가상 환경 사용하기 (0) | 2023.12.25 |
